Priority-Based Connected Components

Malware News
1

Refined Connected Components with Edge Priority and Size Limit

Source: Picture by Macrovector on Freepik

Graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A Graph is made up of nodes/vertices and edges. Nodes denote entities in the graph data while edges represent a relationship between nodes.

Nodes can be cities, items/products, or entities (green dots in the image). The edges (the lines between the green dots in the image) are the relations that link these nodes, for example, nodes can be products, and the edge between products can be their category.

Graph-Structure

Connected Components and Need to Refine it

In Graph theory, a component of an undirected graph is a subgraph in which any two vertices are connected by paths, and which is connected to no additional vertices in the rest of the graph. Breadth-first search or Depth-first search are utilized to compute the components of a graph in linear time.

Source: Wikipedia, Graph with three connected-components

So far we have seen Graphs and Connected components. The Connected component algorithm is utilized in many fields to connect entities depending on the linking edges. The connected components have their application in computer vision for region detection/blob extraction. Connected components are also used in topological sort to solve problems like scheduling jobs from given dependencies. Connected components can also be used in detecting cycles in a graph and solve problems like circular payment or money laundering for financial sectors.

While it is definitely a very useful algorithm but at times we have seen that there is a need to refine the algorithm to adjust the priority of edges and limit the size of the components. Let me list down a few scenarios in which this can be realized and clarify what we mean by priority and limiting the size of components.

Scenario-1

For a Retail company, there may be a need to group similar items to provide customers better item substitution options for out-of-stock scenarios. For this, we’d need to define groups of similar items. Items to be considered a group may in turn be defined by the criteria below.

  1. Item description similarity (Priority-1, top priority)
  2. Category description similarity & pricing similarity (Priority-2)
  3. Department description similarity & buying pattern similarity (Priority-3, lowest in terms of priority)
Items can get linked by any one of the above criteria, but linking items by priority criterion are preferred. Apart from this, there can be additional constraints such as a maximum of ‘X’ items in a group (avoids groups from getting too broad or unwieldy) and an item can be part of only one group (ensures groups are mutually exclusive).

If we use a vanilla connected component algorithm like a DFS(Depth-first search) or a BFS(Breadth-first search) with a limit of ‘X’ (breaking connected component when the size reaches ‘X’), we may end up with heterogeneous groups, i.e. many items across categories within the department may get linked. We need to minimize such cases and optimize the defined priorities as well.

Product from walmart.com

Other Scenarios

Similar use cases can arise in customer care centers where companies assign care agents based on their skillsets and defined priorities. The above-stated scenarios are types of Smart-Agent Assignment problems.

Picture on Freepik
In the above scenarios we see there is a need to run connected components but first connect entities with higher priority edges and then move to lower priority ones. Also, apart from it, every group needs to have a size-limit.

To tackle similar analytical challenges as the above we have come up with an algorithm to adjust the priority of edges and limit the size of the components.

Priority-Based Connected Components Algorithmic Details

  1. The algorithm provides users an option to input the visiting order of the nodes, ‘visit_order’. If the user doesn’t provide any order, the nodes will be visited in the order of incoming edges in the Graph.
  2. The algorithm iterates the priorities in decreasing order, i.e (Priority 1 > Priority 2 > … > Priority n). Within each iteration, nodes are selected in the ‘visit_order’, defined in step-1.
  3. For the node ‘X’, perform a union operation (connecting nodes) with its neighboring node (where exists an edge between this node and ‘X’) having priority ‘p’, such that ‘p’ is the current highest priority. This is efficiently done using a Disjoint-set union data structure. It may be possible that at some point, ‘X’ and the neighbor are not individual nodes but sub-graphs. In that case, the two subgraphs will merge and become part of one component.
  4. If ‘X’ has no more edges connecting a neighbor with priority ‘p’, move to the next node in the ‘visit_order’.
  5. Once all the nodes are visited, perform step-3 & step-4, for the next highest priority.
  6. If at any stage the number of elements in a component reaches the threshold (Default value = 100, can be modified by the user), there won’t be any more changes/linkages for that component.
for priority in priorities:
    for X in visit_order:
        for Y in neighbour_of_X:
            if edge_priority[X,Y] == priority:
                Union(X,Y)

Let’s see how this algorithm will work with an example. The threshold here is set to 3, limiting the size of components. Dotted edges denote the link and priority associated.

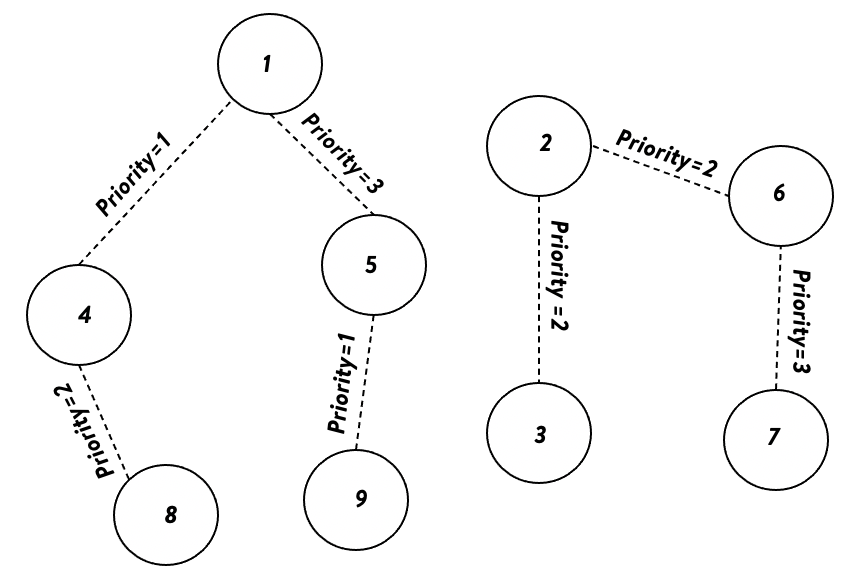Graph and Linkages, Threshold=3

At the first iteration, all nodes having edges with Priority-1 get connected.

1–4 and 5–9 gets connected

In the next iteration, the algorithm connects nodes with edges between them of Priority-2.

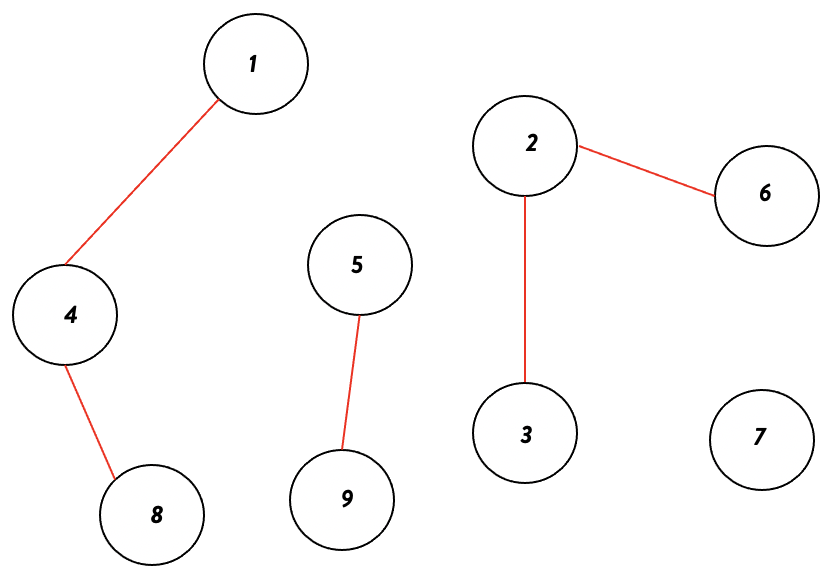1–4–8 gets connected, 2–3–6 gets connected and both reach the threshold

The algorithm stops as the threshold is reached for components and no more edges are left. Above are the final connected components with the set threshold and provided edges priority.

Our Open-Source Library that can be utilized

We have open-source this work to Walmart public GitHub. Here is the link to the project repository.

GitHub - walmartlabs/priorityY: Priority Based Connected Components

We have also released the library in pypi.org as a pip-installable package which can be downloaded here.

Installation

pip install priorityY

Usage

If we are to implement the example shown earlier using priorityY package then we’d use the following syntax.

from priorityY import *
G = [(1,4,1),(1,5,3),(2,3,2),(2,6,2),(6,7,3),(4,8,2),(5,9,1)]
threshold = 3
components = priority_based_linkage(G,threshold)
print(components)

Output

[[1, 4, 8], [2, 3, 6], [5, 9], [7]]

The ‘visit order’ of the nodes is an optional parameter. The algorithm iterates the priorities in decreasing order and within each iteration, nodes are selected in the ‘visit_order’ if provided else in the order of incoming edges in the Graph.

# visit_order provided
components = priority_based_linkage(G,threshold,[3,4,1,5,2,9,8,7,6])

priorityY

Benefits Realisation

We performed a baselining of a Priority-based connected Algorithm with an existing DFS-based approach in one of our data science application which was designed to stop connecting nodes when the threshold is reached without taking priority into account. We calculated 3 metrics and realized a significant improvement in each one.

  1. Quality Gain Percentage: This metric calculates the percentage improvement in the quality of connected components. The greater the number of high priority edges playing role in forming the connected components, the higher is the quality.
  2. Mean Quality Gain Percentage per Component: This metric calculates the percentage improvement per component and takes an average of quality gain percentage across all components.
  3. Percentage Reduction in the number of components hitting the Threshold: We wanted to minimize the number of components explicitly hitting the threshold.

Conclusion

This blog post looked at a refined version of connected components that takes priority of edges into account and limits the size of the components depending on the use case needs.

We have exposed this functionality as an open-source package, that can be utilized at work. The source code is also out there for teams to extend the capabilities if required. I would like the thank my team Pravesh Garg, Somedip Karmakar, and Subhasish Misra for being there throughout the process of ideation and validation of the work. Also, we are grateful to our Engineering counterparts for helping us with the pipeline and making the feature available over Dashboard.

Thanks to Oscar Blass, Cory Stegemoller, and Meriah Montondo for helping us out with the open-source process.

References

Priority-Based Connected Components was originally published in Walmart Global Tech Blog on Medium, where people are continuing the conversation by highlighting and responding to this story.

Article Link: Priority-Based Connected Components | by Abhishek Mungoli | Walmart Global Tech Blog | Medium