Everyone loves Elliptic Curve Cryptography (ECC). And by everyone, I mean the Internet as a whole. For the first twenty years of Internet security, the RSA public key algorithm was nearly the only choice among asymmetric encryption algorithms (with DSA/DSS being the red-headed stepchild). But today, all modern browsers, and the majority of SSL/TLS servers on the Internet prefer Elliptic Curve Cryptography to RSA.
RSA had different key sizes (512, 1024, 2048, 4096) that mapped to the number of digits of a prime random(ish) number to denote cryptographic strength. ECC has different curves. Curves are more complex than just the size of a prime number; they describe finite fields that will be used to compute public and private keys. Some curves are better than others, and they are competing in the cryptographic marketplace of the Internet. Let’s take a look at which ones are hot right now, and take a peek at the up-and-comers.
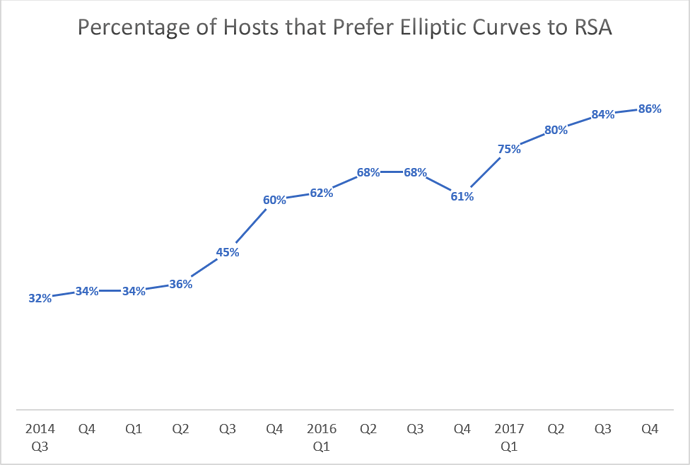
The following data comes from the ongoing F5 Labs research effort called the TLS Telemetry Project. The project samples TLS connections from both the Internet at large and the list of a million popular websites (the union Alexa and OpenDNS one-million lists).
We publish an annual TLS Telemetry report and gather cryptographic data every quarter. Recently we have started collecting the curve type preferred by each TLS server that we connect to. This particular sample looks at 320,000 TLS hosts within the OpenDNS Top 1 million list.
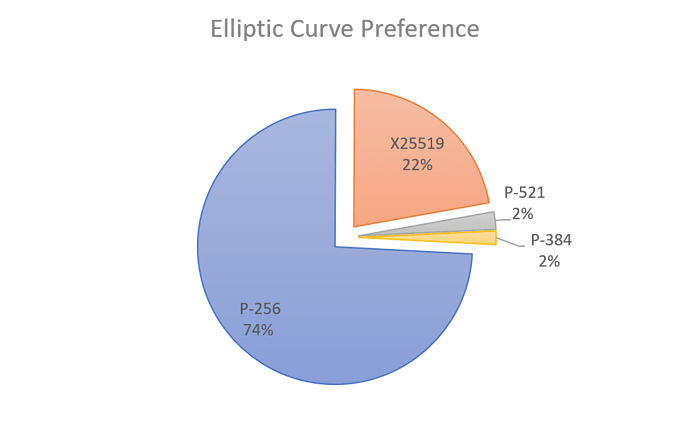
As you can see, the most popular (preferred) elliptic curve is NIST P-256, followed by X25519.
Let’s try to describe the difference between these curves and look at a few others that might be popular in the coming years. To make the comparisons more approachable, let’s identify which pop singer would represent each curve. (This is how my mind is working right now; my last piece compared the Mirai botnet to Madonna. Maybe it’s because my doctor changed my meds?)
The images below are taken from Dierdre Connolly’s inspiring talk1 on getting involved with Elliptic Curve Cryptography.
The Standard Curve, NIST P-256, is Beyoncé
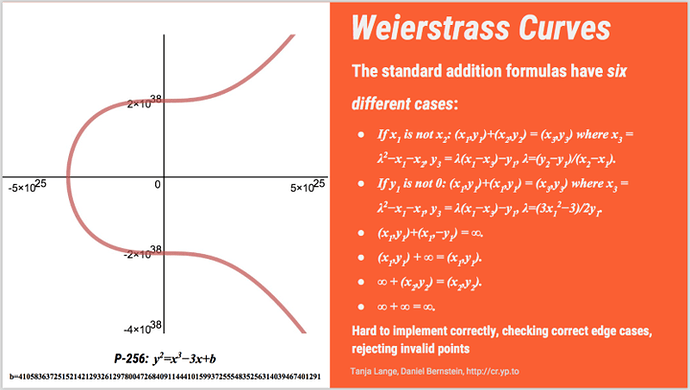
Like Beyoncé, Curve NIST P-256 is the chart topper. She’s the current diva of the elliptic curve movement. P-256 is an old Weierstrass curve, part of NIST’s Suite B playlist, and is still the only curve that is supported in the FIPS 140-2 specification. You might also know P-256 as prime256v1.
NIST P-256 is the best curve for interoperability, and people have spent a lot of time optimizing and promoting it. There is hardware acceleration support for P-256, but that is a smaller factor for the Internet as a whole as virtual machines take on more and more TLS termination. Intel CPUs have no special instructions to support P-256, anyway.
Three quarters of the Internet prefers P-256 to other curves, and that’s probably because it’s the default curve for OpenSSL, which is the default TLS stack for the Internet.
Even with her name recognition and broad support, P-256 might start seeing some decline as she becomes long in the tooth. She has some baggage; because of her origin from NIST (and by association, the NSA), some claim that P-256 may have a cryptographic back door. Similar claims were made about NIST’s pseudo (sorry, I meant deterministic) random function DUEL_EC_DRBG,2 which also used elliptic curves. Equating DUEL_EC_DRBG to Beyoncé’s cheating husband, Jay-Z, stretches our analogy to its limit.
Both the DUEL_EC_DRBG and P-256 rely on “magic numbers” chosen by their designers. There is speculation that those magic numbers are derived from some special values known only to those designers that would allow them to decrypt any TLS connections using them. Neither DUEL_EC_DRBG nor P-256 are provably secure.
If you look at http://csrc.nist.gov/csrc/fedstandards.html, you'll see NIST stating "These curves have been generated and reviewed by the government.”
“Offhand I can’t think of a NIST document admitting that the curves were created by NSA, but everyone in the community knows Jerry Solinas as the NSA point man on this. NSA’s earlier contribution of the same curves to X9 is what led to X9 demanding seeds for curves (and incorrectly labeling seeded curves as ‘verifiably random’).” —D. J. Bernstein, Research Professor, Computer Science, University of Illinois at Chicago
The whole concept of these “magic numbers” has its own acronym: NUMS—nothing up my sleeve.3 And if there is a thematic conspiracy theory in the elliptic curve sphere, it is accusations around the construction of these magic numbers. Here’s an interesting example—check out Oleg Gryb’s manifesto, Why I don’t Trust NIST P-256, in which he compares cryptography’s favorite characters, Alice, Bob, and Eve, to specific actors in the crypto community.4
Partly because of queasiness surrounding this crypto scandal, there are newer pop stars on the crypto horizon.
X25519: The Cardi B of Elliptic Curves
Like Cardi B, X25519 is on everyone’s Spotify right now, and she’s getting big fast. She may even eclipse Beyoncé herself someday.
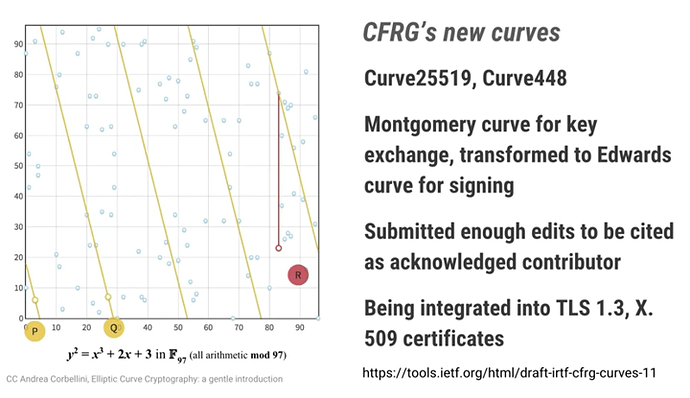
X25519 describes a Diffie-Hellman key exchange with the curve described by the prime number 2255-19. X25519 has a lot of things going for it:
- First, it is designed by Daniel J. Bernstein (DJB) himself, and the source code5 is public domain (woot!) and the algorithm has no patents. DJB claims it is provably secure (that is, it doesn’t rely on magic numbers). By design, it’s immune to known timing attacks (beware, famous last words).
- It is recommended by the IETF TLS committee and, most recently, NIST publicly stated that they are behind X255196 (they had been saying the same at the meetings earlier, but this is now official).
- X25519 has 40% lower computational complexity than P-256. Virtual machines should prefer it to P-256. The lower complexity also means that it will be easier to do on low-CPU devices like the billions found in the Internet of Things (IoT).
- Because X25519 is so awesome, it’s already supported by most major browsers, TLS vendors, clouds, and CDNs.
We expect that everybody who implements TLS 1.3 will implement X25519. We could elaborate on the rationale but, in short, anyone who doesn’t will be losing the performance benefit of TLS 1.3 and essentially doing TLS 1.2 as far as message flow and thus have higher latency.
Ed448 is Goldilocks, P-384 is Támar Davis, and P-521 is Farrah Franklin
No, “Goldilocks” is not a rapper like Chance the Rapper; I refer here to the story of Goldilocks and the Three Bears. Recall that Goldilocks liked her porridge not too cold and not too hot, but just right. Ed448 aims to meet some similar midpoint by using the “Goldilocks” Solinas trinomial prime (p := 2448 − 2224 − 1).
Ed448 is an Edwards curve, which has simpler maths than Weierstrass curves, and can also be used for elliptic curve digital signatures (certificates).7 It’s not represented in a measurable form in our scanning data, but it is worthy of some discussion here, as it relates to P-384, which is current preferred by about 2% of TLS hosts among the OpenDNS top 1 million.
P-384, also called secp384r1, is another NIST-approved Suite B elliptic curve with a larger key size (384 bits—duh). P-384 has a performance penalty of about a factor of three over P-256, and a few dozen extra bytes on network in a handshake.
The intent of both P-384 and Ed448 is to provide higher security than that of P-256 and X25519. However, it’s hard to achieve higher security because the key exchange is just one part of TLS. The higher key exchange security needs to be matched diligently throughout TLS with higher strength symmetric keys (like AES256 instead of AES128, and SHA512 instead of SHA256, for example). Whether that higher security is accomplished throughout or not, there will be a performance penalty for P-384 and Ed448. At this time, it seems most of the Internet is content with the 128-bit security offered by P-256 and X25519.
Currently Suite B has P-384, not P-521 nor Ed448. Suite B is, itself, in the transition period out of ECC toward quantum-safe algorithms. But even with the Suite B stamp of approval, P-384 hasn’t taken off and isn’t likely to. No notable effort has gone into optimizing P-384, so we have a double hit: the higher complexity of P-384 and fewer optimizations. When looking at these factors, if pushed to support one or the other, vendors will likely choose to do Ed448 in TLS over P-384.
Like P-384, about 2% of hosts prefer P-521, which offers even higher security strength. But P-521 isn’t likely to take off for the same reasons as P-384.
There isn’t much interest in higher strength curves, at this point. There is some interest to support higher finite fields (DH, not ECDH). For those that want X.509 certs with higher strength, P-384 is the only option. However, we need P-384 more in ECDH than in X.509 certs due to the quantum computer threat.
There is an effort on the part of some CAs, though, to add EdDSA with Ed448. It makes sense if you are a CA to introduce EdDSA with Ed448 rather than deal with X25519 + EdDSA.
For the record, both Támar Davis and Farrah Franklin were also members of Destiny’s Child with Beyoncé, but their careers did not reach the same height. Just like P-384 and P-521 are good, but not as popular as P-256.
Agreeing on a Curve: Theory vs. Reality
In theory, it is up to the TLS client to choose the curve. It sends a list of curves it supports to the server, and the server is supposed to pick the most secure and then agree to it. In reality, the server has its own private order, usually preferring speed or cost, and then it says, “Okay, cool, I can do P-256.” Ahhh, the innocence of the IETF committee design.
So, What is the Best Curve?
The Internet now relies on these maths that are so complicated that you have to be smarter than me to understand them (admittedly that’s not saying much, but it’s something). So, most of us can’t make a technical judgement about which elliptic curve is better. We have to decide by reputation of the character championing the curve.
If that’s the case, then we should probably go with X25519. It’s champion, Daniel J. Bernstein, is beyond reproach, in my book. He’s even defined a model for “safe curves” (NUMS), which you can see at SafeCurves.8 And, if you agree with my endorsement of DJB’s X25519 algorithm, then you’re choosing a finite field elliptic curve function based on the recommendation, not on its technical properties, or the reputation of its champion, but the reputation of my character. Funny how humans work. “Like” for X25519.
Article Link: https://f5.com/labs/articles/threat-intelligence/ssl-tls/everyone-loves-curves-but-which-elliptic-curve-is-the-most-popular